Why do we use Degrees?
When we think about angles, the first thing that comes to mind is degrees. Examples are 30°, 45°, 90°, 360°, etc. However, have you ever wondered why we define angles in this way?
The answer lies in the properties of 360°. This number is special as it can be divided exactly by no more than 24 numbers (ie. 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360). In consequence, if we use 360° to represent the angle that covers the full circle, a lot of pieces of the circle will have “nice” angles.
For example, half a circle is represented by 180°, a third by 120°, a quarter by 90°, a sixth by 60° and so on. However, this choice is arbitrary. Nothing is stopping us from making the angle that covers a full circle 50 new degrees and having half being 25 new degrees. Let’s represent new degrees using ![]()
Let’s find the conversion factor to go from usual degrees ![]() to new degrees
to new degrees ![]() for the angle
for the angle ![]() :
:
![]()
If we multiply this factor by 90° we’ll see how much this angle is worth in new degrees:
![]()
This value is exactly what we would expect.
What are Radians and Why do we use them?
Now that we have established that we can choose how to measure our angles arbitrarily, we should be wondering if there is a superior way of measuring angles. The answer is, that it depends on what you are working on. Let’s see an example. Let’s say you want to find a formula to relate an angle with the arc it forms in a circle of radius r.
In this graph we show the arc (in green) formed by the 45° angle (called ![]() ) in a circle of radius
) in a circle of radius ![]() (in blue):
(in blue):
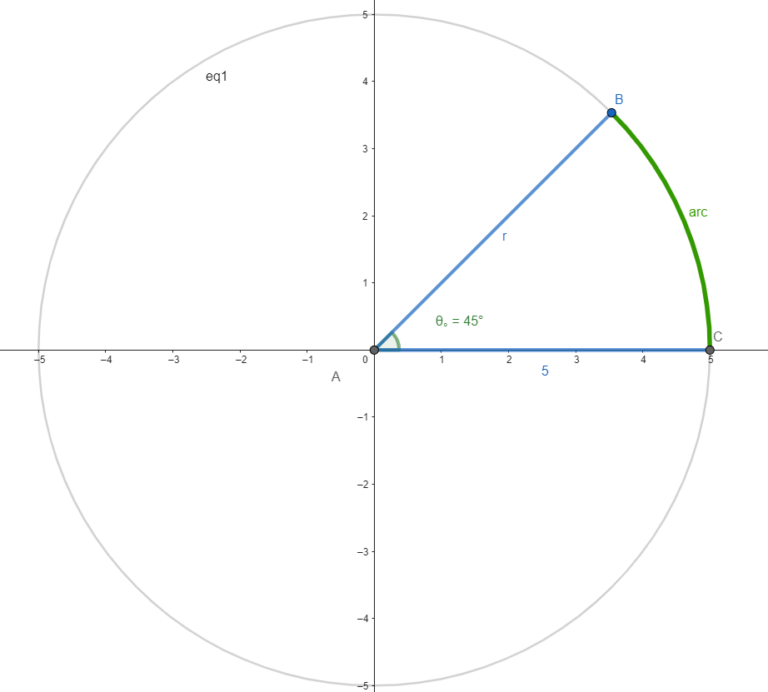
We can find a formula to calculate the arc algebraically like this:

Where ![]() is the arc that the angle
is the arc that the angle ![]() forms in a circle of radius r. This formula is extremely useful, but can this formula be simplified?
forms in a circle of radius r. This formula is extremely useful, but can this formula be simplified?
Let’s see what happens if we transform the angle ![]() to new units using the conversion factor
to new units using the conversion factor ![]() that transforms the angles from degrees to a new unknown unit. In our new units, our angle will be:
that transforms the angles from degrees to a new unknown unit. In our new units, our angle will be:
![]()
Using this in our formula we obtain:
![]()
Now we remember that we are free to choose ![]() to be anything as we are free to choose the unit we measure our new angle with. Why not make it such that it cancels the constant in the front? Let
to be anything as we are free to choose the unit we measure our new angle with. Why not make it such that it cancels the constant in the front? Let
![]()

This formula looks cleaner! The arc length is just the radius of the circle times the angle in this new unit that transforms from degrees using the conversion factor ![]() . This means that in this new units
. This means that in this new units ![]() is equivalent to
is equivalent to ![]() ,
, ![]() is equivalent to
is equivalent to ![]() and
and ![]() is equivalent to
is equivalent to ![]() .
.
This new unit is so important that it received its own name the radian. Using our new improved formula we can see that for 1 radian:
![]()
So 1 radian is the angle that forms an arc equivalent to the radius.
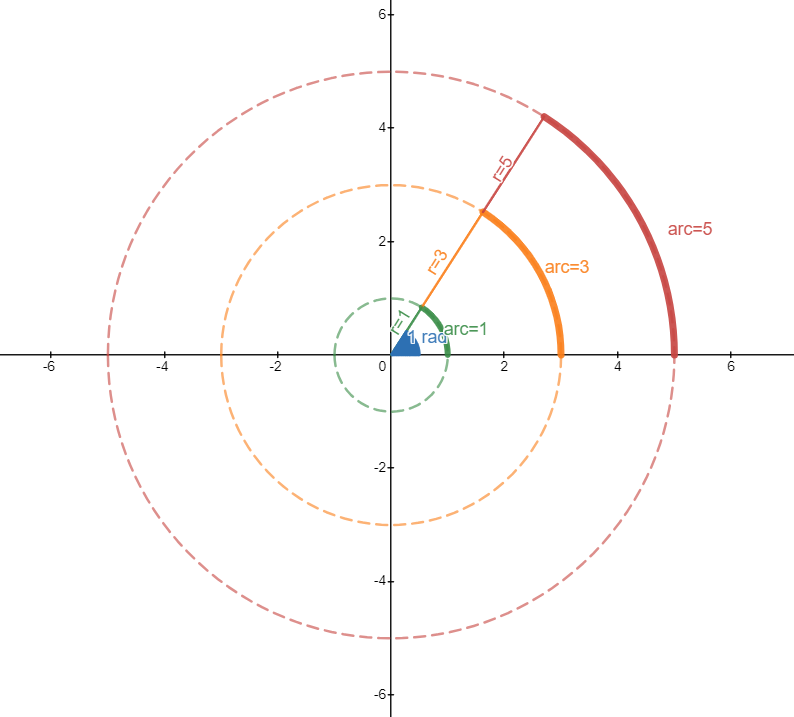
Radians are really important in Calculus and Physics so it is imperative that students learn to do everything they can do with usual degrees with radians and to naturally move from one to the other. Let’s see some examples of how to transform some angles.
Transforming from Degrees to Radians:
To transform from degrees to radians, we simply need to multiply the angle in degrees times the transformation factor ![]()
Transform ![]() to radians:
to radians:
![]()
Transform ![]() to radians:
to radians:
![]()
Transform ![]() to radians:
to radians:
![]()
Transforming from Radians to Degrees:
To transform from degrees to radians, we simply need to multiply the angle in radians times the inverse of the previous transformation factor ![]()
Transform ![]() radians to degrees:
radians to degrees:
![]()
Transform ![]() radians to degrees:
radians to degrees:
![]()
The study of radians is extensive and we could talk about them for a long time like learning how to use trigonometric rations like ![]() and
and ![]() with them, but for now, knowing where they come from and how to transform from degrees to radians is enough to get started.
with them, but for now, knowing where they come from and how to transform from degrees to radians is enough to get started.
This has been a brief introduction to the concepts of quadratic equations. For more information on this topic as well as assistance with homework and test preparation, feel free to reach out to an Academic Director toll-free at 1 (877) 545-7737 or via our Contact Us page.
Powered by WordPress with QuickLaTeX