What is the Unit Circle?
The unit circle is a tool that allows us to define and calculate some trigonometric ratios (sin, cos, tan, etc.) and uncover some relationships between these ratios with ease.
As its name suggests, it is a circle with a radius of one. This means that if you take a string of length one (it could be 1 m or 1 cm, or any unit) and hold one end of the string fixed while rotating the other, you would have draw a unit circle.
To understand the relationship between the unit circle and trigonometric ratios, we must choose a random point in the circle. Let’s call this point ![]() . The angle formed between the positive x-axis and the line joining the center to the point
. The angle formed between the positive x-axis and the line joining the center to the point ![]() will be called
will be called ![]() . As we change
. As we change ![]() around the circle, you can see that we can get any angle you want.
around the circle, you can see that we can get any angle you want.
Nevertheless, this property is not unique to the unit circle (we can do this with any circle), so what is so special about this circle?
Why is the Unit Circle Special?
Now that we have our angle ![]() and our point
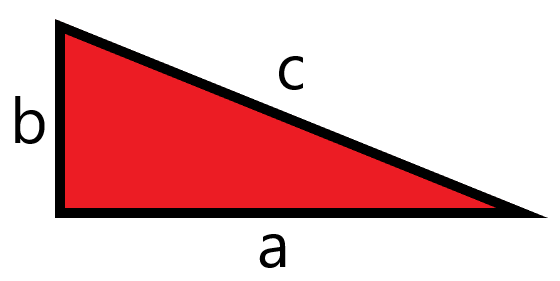
and our point ![]() we can build a right triangle by tracing a line perpendicular to the x axis, that passes throw the point
we can build a right triangle by tracing a line perpendicular to the x axis, that passes throw the point ![]() .
.
We observe something quite interesting in this triangle, the hypotenuse of all of these triangles is one! It does not matter which angle you use, they all have this property.
This may not look like a big deal, but when you try to calculate trigonometric ratios this changes everything.
Calculating trigonometric Ratios
The formula to calculate the sine and cosine for an angle are:
![]()
Since the hypotenuse is one, and knowing that the lengths of the opposite side of the triangle is ![]() and the adjacent is
and the adjacent is ![]() , we obtain
, we obtain
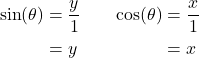
Notice that ![]() is equal to
is equal to ![]() while
while ![]() is equal to
is equal to ![]() . Wait a second, those are exactly the coordinates of the point we chose to form theta. That means that our point can be written as
. Wait a second, those are exactly the coordinates of the point we chose to form theta. That means that our point can be written as ![]() . With this notion now we can define the trigonometric ratios of any angle without using right triangles.
. With this notion now we can define the trigonometric ratios of any angle without using right triangles.
Trigonometric functions for angles bigger than 90°
Ever wonder how is it possible to find the ![]() for
for ![]() ? This is a valid question. Sine is in fact opposite over hypotenuse, but you can only have a hypotenuse in a right triangle. However, if the angle is bigger than
? This is a valid question. Sine is in fact opposite over hypotenuse, but you can only have a hypotenuse in a right triangle. However, if the angle is bigger than ![]() then what is the hypotenuse of a triangle containing this angle. The answer is, it does not exist.
then what is the hypotenuse of a triangle containing this angle. The answer is, it does not exist.
We can solve this using the unit circle. We can generalize the property of angles in the first quadrant ![]() and say that this is true for all angles. That is, the point
and say that this is true for all angles. That is, the point ![]() in the circle contains the
in the circle contains the ![]() in the position of
in the position of ![]() and the
and the ![]() in the position of
in the position of ![]() .
.
Therefore, if you are asked for the sine of ![]() then you draw the angle, draw the unit circle and find the point
then you draw the angle, draw the unit circle and find the point ![]() where the angle connects to the circle. In the case of
where the angle connects to the circle. In the case of ![]() that point is
that point is ![]() based on our definition then
based on our definition then ![]() and
and ![]() .
.
Amazingly, in this example, we have the cosine of an angle being negative and the sine being zero, something impossible under the usual definition of the trigonometric ratios.
In fact the unit circle definition of sine and cosine is the standard way that mathematicians use to define these ratios.
What about Tangent?
I know what you must be thinking now, sure defining sine and cosine like this is good, but what happened to tangent? This is still defined as:
![]()
We could stop there, but notice that if we input this using the unit circle property ![]()
![]()
And now you could extract the tangent from sine and cosine that are now well defined for all angles.
This is great, but there is a way to see the tangent directly from the unit circle.
Consider the following picture
Notice that this is the same unit circle as before, but now we draw a line tangent to the circle and we expand the radius to form a bigger right triangle. Using this triangle now we can calculate the tangent of the angle
![]()
So the length of t (that comes from the tangent line) in the unit circle is equivalent to the tangent o an angle. And that is where the name tangent comes from. It is literally the tangent.
The unit circle makes the trigonometric rations appear in front of your eyes.
What Else can I Learn from the Unit Circle?
Did you notice that we found a relationship between tangent and sine and cosine? When you relate trigonometric ratios, the relationship is called an identity.
For example, the identity we found before is a quotient identity, as you found a relationship by diving trigonometric ratios.
![]()
With the unit circle we can find one more identity. If we go back to our first triangle, we can use Pythagoras’ Theorem to find the following relationship
![]()
Using again the property ![]() we find
we find
![]()
Wow, if you add the square of the sine and the square of the cosine of any angle you get one! This property is unintuitive, but really useful in certain situations, allowing us to change from sine to cosine at will. This property is called a Pythagorean Identity.
Similar identities can be found if we use our second triangle (Hint: the hypotenuse is the secant of the angle) therefore:
![]()
Isn’t that relationship interesting?
The Unit Circle is Amazing
As we have seen, the unit circle can offer you new information that sometimes is hard to see if you use circles of different radii. However, the best application of the unit circle is its intimate relationship with trigonometric ratios. If you master the unit circle’s properties, then you will be a master of trigonometric ratios and identities, so spend some time memorizing them. It is also useful to try exploring them by yourself by drawing all different types of triangles using an angle, a point in the unit circle, and a line perpendicular to the x-axis or the y-axis.
This has been a brief introduction to the concept of the unit circle. For more information on this topic, as well as assistance with homework and test preparation, feel free to reach out to an Academic Director toll-free at 1 (877) 545-7737 or via our Contact Us page.
Powered by WordPress with QuickLaTeX